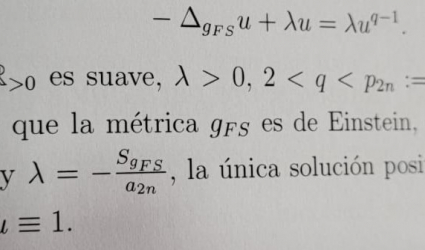Lo que hacemos

Este proyecto pretende ofrecer oportunidades de formación continua a docentes que laboran en escuelas públicas. Se pretende fomentar el desarrollo del pensamiento numérico en los docentes de manera que puedan innovar con nuevas estrategias para la enseñanza de temas presentes en el plan de estudios oficial del Ministerio de Educación.

Unidad  a la que pertenece el proyecto: Sede de Occidente

Vigencia: 01/08/2020 al 31/12/2022

Responsable: Dra. Patricia Maroto Vargas.

Este proyecto se centra en proponer, emplear y desarrollar diversos aspectos matemáticos y numéricos, principalmente los métodos de elementos finitos mixtos y esquemas de Galerkin, con el propósito de analizar la solubilidad de problemas lineales y no-lineales (modelados por sistemas de ecuaciones diferenciales parciales), los cuales representan diversos fenómenos propios de la biomedicina, física e ingeniería, entre otras disciplinas.

Unidad de Investigación a la que pertenece el proyecto: Sede de Occidente

Vigencia: 01/08/2020 al...

Este proyecto está dedicado al estudio de existencia y multiplicidad de soluciones de ecuaciones elípticas no lineales de tipo Yamabe, sobre ciertas variedades Riemannianas cerradas (compactas y sin borde), conocidas como espacios simétricos compactos de rango uno.

Unidad de Investigación a la que pertenece el proyecto: Sede de Occidente

Vigencia: 03/03/2020 al 31/12/2022

Enlace al proyecto: https://vinv.ucr.ac.cr/sigpro/web/projects/C0084

Investigador Principal: Dr. Héctor Mauricio Barrantes González.

Este proyecto de investigación está orientado al desarrollo de métodos numéricos para simular numéricamente flujos incompresibles con transferencia simultánea de calor y masa en el marco de aproximación Oberbeck-Boussinesq; un modelo constituido por un sistema tipo Navier-Stokes acoplado no linealmente con ecuaciones de advección-difusión que describen el transporte de la temperatura y la concentración de una cierta sustancia en un fluido viscoso e incompresible. Este modelo matemático permite modelar muchos fenómenos de interés en dinámica...